Plato’s Elements in Flatland

The Greek philosopher Plato associated three-dimensional objects, the so called regular convex polyhydra with the four elements Fire, Air, Water and Earth. Only five convex regular polyhydra exist in three dimensions, the tetrahedron representing the element fire, the cube for the earth element, the icosahedron for water and the octahedron for air. The fifth polyhydron, the dodecahydron was seen as representing the element of the fabric of the cosmos. The two-dimensional faces of these polyhydra, as well as the so-called vertex figures of these three-dimensional objects, are the regular polygons the equilateral triangle with angles of 60 degrees, the square with angles of 90 degrees and the pentagon with angles of 108 degrees.

Painting

In a creative expression mood, I painted the faces of the four elements on a wall in my new office space. It can be seen as a projection onto two-dimensional space, like “flatland”. The painting shows air in earth in water in fire. Air in earth depicts the earth-air duality as is so elegantly shown in the cube-octahedron duality with interchanging vertices and faces of the object.

Design

The design phase included calculated drawings of the various triangles with their angles and line segments. The design was then drawn on the wall with a pencil, ruler and compass. A construction as it should be done. 😉

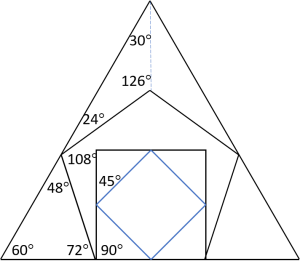
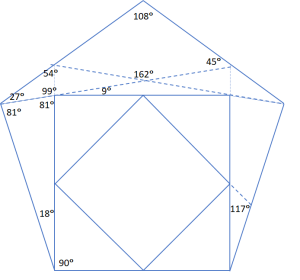
Considering integer valued angles only, note the divisibility by three of all angles shown in the two figures above, and almost all angles are divisible by nine. The angles of the triangle and the square are also divisible by five, whereas the angles of the pentagon are not. More intricate properties are satisfied by the angles shown in the above figures, especially the numerological connections. For example, with the exception of the 99-degree angle, numerical values of the angles belong to a special class of numbers of which there are relatively few. These numbers, as well as all numbers obtained by permutation of their decimal digits, are divisible by the total integer sum of their digits.

The triangle with angles of 81-81-18 degrees is exactly one segment of a 20-gon, a polygon with twenty vertices, twenty edges and twenty angles of 162 degrees.

Some Trigonometry

The equilateral triangle gives exact expressions for the goniometric functions of angles of 60 and 30 degrees, the square for 90 and 45 degrees, the pentagon, by its construction, for angles of 108, 72 and 36 degrees. Goniometry, or trigonometry, defines mathematical functions such as sine, cosine and tangent of angles. These functions are in fact ratio’s (proportions) of line segments in triangles. The word “exact” means that the values of the goniometric functions can be expressed by square roots of integer numbers. For example, the cosine of 45 degrees equals ½√2 , the cosine of 30 degrees equals ½√3, the cosine of 36 degrees equals ¼(1+√5). The latter follows from the construction of the pentagon. Triangles play a most important role in Plato’s cosmogony as laid down in his dialog with Timaios. A role that resembles that of elementary particles in modern physics.

Most of us have some recollection of math classes from secondary school, so we know that simple formulas exist for computing the sine and cosine of the sum and difference of two angles, using the two angles’ sine and cosine values. The trigonometric functions for half angles have simple expressions too. As the angles of 30, 36, and 45 degrees are triplicates, the sines and cosines of all angles with values divisible by three can be expressed in the values of the angles of 30, 36, and 45 degrees. To refresh your memories the formulas are given here.

Let a and b denote angles, then the following formulas hold:

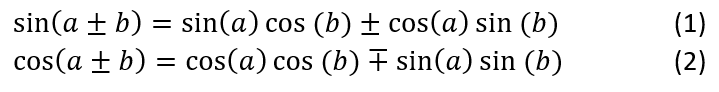
Taking b = a the second formula becomes cos(2a) = cos²(a) – sin²(a) .

By using cos²(a) + sin²(a) = 1 , which results from the Pythagorean theorem, it follows that cos(2a) = 1 – 2sin²(a) = 2cos²(a) – 1. From these equations the formulas for half angles are easily obtained by replacing a with ½a and taking the square root:

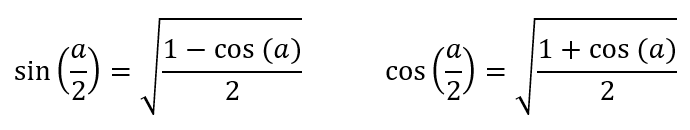
Some examples:

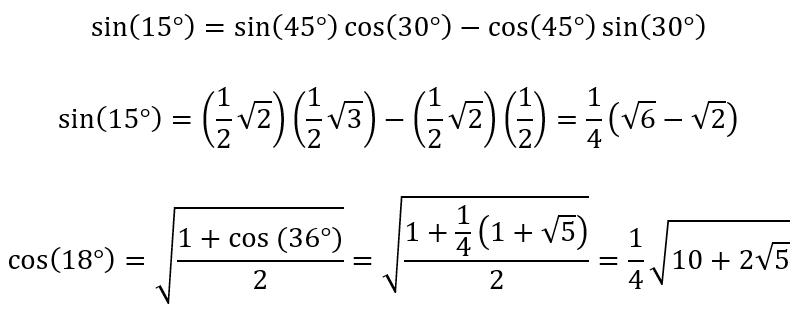
Applying the sine rule (see https://en.wikipedia.org/wiki/Law_of_sines), the line segments of the triangles are determined. However, the line skeleton of the wall painting can be constructed without using trigonometric functions! You only need a ruler and compass.

Construction

The construction involves drawing pencil lines with ruler and compass. We first construct the pentagon, then the square inside it with the smaller square inside at 45 degrees. Next the left (or right) 60°- 72° – 48° triangle is constructed and copied to the other side. Finally, the fire triangle is completed. The various triangles can then be painted.

The pentagon

Shown in the figure below.

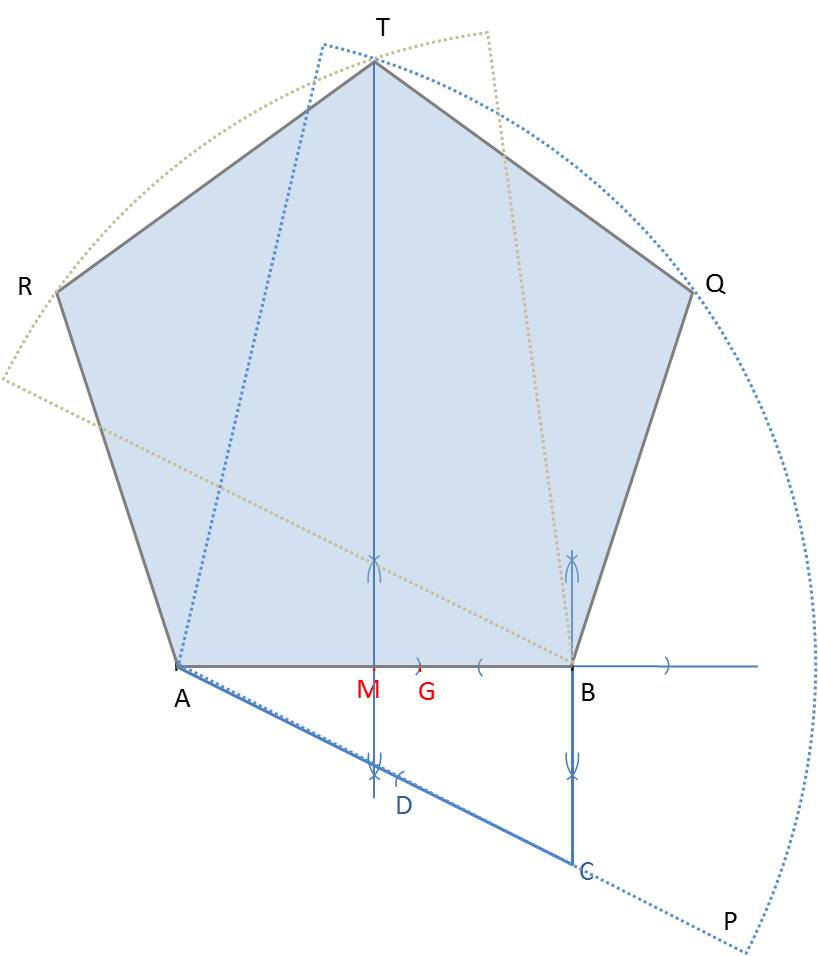
Draw the line segment AB and construct the perpendicular bisector. M denotes the middle of AB. A and B are vertices of the pentagon.
Construct a perpendicular line in point B pointing downwards and measure out BM onto this line to obtain point C.
Draw the line AC and extend it downwards. Measure out BC from C onto this extended line AC to obtain point P.
With the compass point in A, circle AP until it intersects the perpendicular bisector through M, constructed in 1. This is vertex T, the top of the pentagon.
Repeat 4. but now with the compass point in B.
With the compass point in A, circle AB until it intersects the circle arc constructed in 5. This is vertex R.
Repeat 6. but now with the compass point in B. This is vertex Q.
Draw the lines BQ, QT, TR, and RA to form the pentagon ABQTR.

The pentagon construction also shows the division of AB according to the Golden Ratio. Line segment CD is equal to BC, and therefore half the length of AB. Applying Pythagoras’ theorem in triangle ABC, we find the length of line segment AC to be equal to ½√5 times the length of AB. Consequently, line segment AD has length -½+½√5. Copying AD onto AB gives point G. The length of GB is 1½-½√5. We see the ratios AB : AG = AG : GB,

1 / (-1½-½√5) = (-½+½√5) / (1½-½√5) = ½+½√5 = 1.618…

The cubes

Construct a perpendicular line in point A and measure out AB on it.
Measure out AB on the perpendicular line through point B, constructed for the pentagon in step 2.
Connect the two upper points of these two perpendicular lines to form the square representing the earth cube
Measure out AM onto these two perpendicular lines.
Connect all intersecting points to form the square at 45 degrees, representing the vertex figure of the air octahedron.

The left 60°- 72° – 48° triangle

We start at vertex R of the pentagon shown in the figure below.

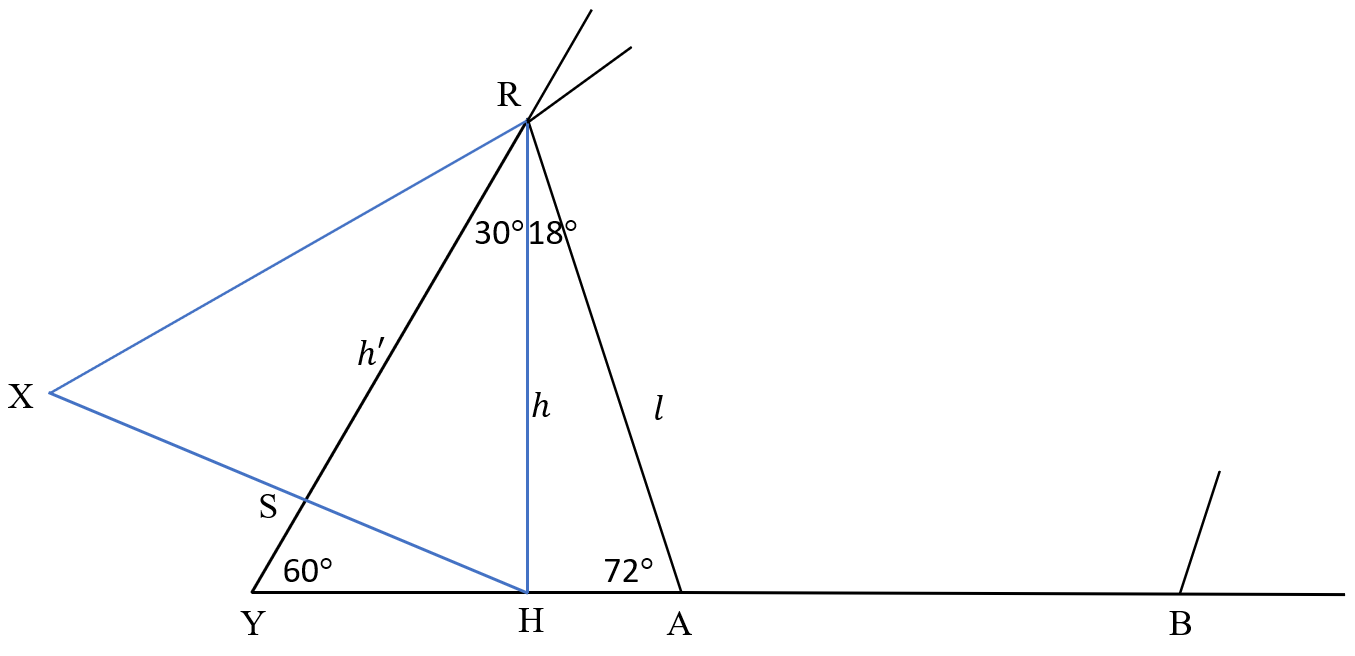
Construct the perpendicular line h from point R onto the extended line BA in H.
Construct the equilateral triangle HRX by circling HR from points H and R. The intersection is at point X.
Construct the bisector h’ of angle HRX and extend it to intersect with the extension of line BA in point Y. This is a vertex of the big equilateral triangle that represents the fire element.
Use the compass to copy triangle YHR to the right side. So, AB is extended with YH, to obtain BZ and a line is drawn from Z to vertex Q of the pentagon.

The figure is completed by extending YR and ZQ to intersect at the top of the big triangle.